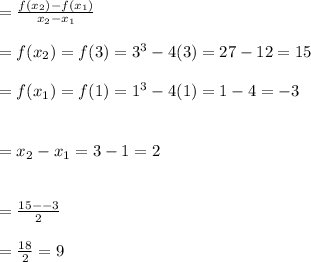Answer:
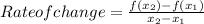
where x₁ and x₂ are values in the interval [x,y] respectively
Explanation:
Well, first to determine the average rate of change of a function, you should have the interval of the values of x for the function.
So lets assume you have a function;
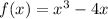
And the interval as [1,3]
Then the average rate of change for the function f(x) will be;
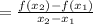
where x₁ and x₂ are the interval coordinates x,y respectively. In this case x₁=1 and x₂=3
To find the average rate of change in this example will be;