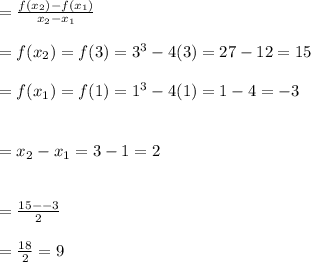Question

How can the average rate of change be identified for a function?

Answer 1

`Rateofchange=(f(x_2)-f(x_1))/(x_2-x_1)`

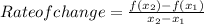
where x₁ and x₂ are values in the interval [x,y] respectively

Explanation:

Well, first to determine the average rate of change of a function, you should have the interval of the values of x for the function.

So lets assume you have a function;

`f(x)=x^3-4x`

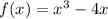
And the interval as [1,3]

Then the average rate of change for the function f(x) will be;

`=(f(x_2)-f(x_1))/(x_2-x_1)`

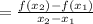
where x₁ and x₂ are the interval coordinates x,y respectively. In this case x₁=1 and x₂=3

To find the average rate of change in this example will be;

`=(f(x_2)-f(x_1))/(x_2-x_1) \\\\=f(x_2)=f(3)=3^3-4(3)=27-12=15\\\\=f(x_1)=f(1)=1^3-4(1)=1-4=-3\\\\\\=x_2-x_1=3-1=2\\\\\\=(15--3)/(2) \\\\=(18)/(2) =9`