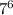Answer:
The equivalent expression is
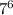 ⇒ answer A
⇒ answer A
Explanation:
* Lets revise some rules of the exponents
- In the exponential functions we have some rules
# In multiplication if we have same base then add the power
b^m × b^n = b^(m + n)
- Ex:
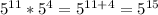
# In division if we have same base we subtract the power
b^m ÷ b^n = b^(m – n)
- Ex:
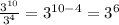
* Now lets solve the problem
- There is the expression

- We have base 7 up and down
∵ In division if we have same base we subtract the power
∵ The base up is 7 and the base down is 7
- We will subtract the powers
∴
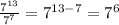
∴ The answer is
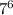
* The equivalent expression is