Question

Suppose that 45% of all adults regularly consume coffee, 40% regularly consume carbonated soda, and 55% regularly consume at least one of these two products. (a) What is the probability that a randomly selected adult regularly consumes both coffee and soda? (b) What is the probability that a randomly selected adult doesn't regularly consume at least one of these two products?

Answer 1

Answer: a) 30% and b) 45%

Explanation:

Since we have given that

Probability that adults regularly consume coffee P(C) = 45% = 0.45

Probability that adults regularly consume carbonated soda P(S) = 40% = 0.40

Probability that adults regularly consume atleast one of these two products P(C∪S) = 55% = 0.55

a) What is the probability that a randomly selected adult regularly consumes both coffee and soda?

As we know that

P(C∪S ) = P(C) +P(S)-P(C∩S)

`0.55=0.45+0.40-P(C\cap S)\\\\0.55=0.85-P(C\cap S)\\\\0.55-0.85=-P(C\cap S)\\\\-0.30=-P(C\cap S)\\\\P(C\cap S)=0.30=30\%`

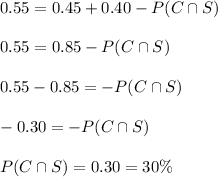
b) What is the probability that a randomly selected adult doesn't regularly consume at least one of these two products?

P(C∪S)'=n(U)-P(C∪S)

`\\P(C\cup S)'=100-55=45\%`

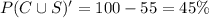
Hence, a) 30% and b) 45%