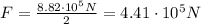Question

A freight train consists of two 8.00×104-kg engines and 45 cars with average masses of 5.50×104 kg . (a) What force must each engine exert backward on the track to accelerate the train at a rate of 5.00×10–2m/s2 if the force of friction is 7.50×105N, assuming the engines exert identical forces?

Answer 1

`4.41\cdot 10^5 N`

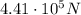
Step-by-step explanation:

First of all, let's calculate the total mass of the train+the engines:

`m=2(8.00\cdot 10^4 kg) + 45(5.50\cdot 10^4 kg) = 2.64\cdot 10^6 kg`

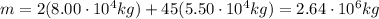
Then we can apply Newton's second law, which states that the resultant of the forces is equal to the product between mass (m) and acceleration (a):

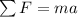`\sum F = ma` (1)

In this case there are two forces:

- The pushing force exerted by the engines, F

- The frictional force,
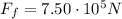`F_f = 7.50 \cdot 10^5 N`, in an opposite direction to the acceleration

So (1) becomes

`F-F_f = ma`

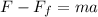
Since the acceleration must be

`a=5.00\cdot 10^(-2) m/s^2`

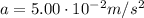
We can solve the formula to find F:

`F=ma+F_f = (2.64\cdot 10^6 kg)(5.00\cdot 10^(-2) m/s^2) + 7.50 \cdot 10^5 N = 8.82\cdot 10^5 N`

However, this is the force exerted by both engines. So the force exerted by each engine must be half this value:

`F=(8.82\cdot 10^5 N)/(2)=4.41\cdot 10^5 N`