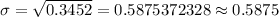Question

Last​ year, a person wrote 126 checks. Let the random variable x represent the number of checks he wrote in one​ day, and assume that it has a Poisson distribution. What is the mean number of checks written per​ day? What is the standard​ deviation? What is the​ variance?

Answer 1

Answer: The mean number of checks written per​ day
`=0.3452`

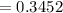
Standard deviation
`=0.5875`

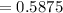
Variance
`=0.3452`

Explanation:

Given : The total number of checks wrote by person in a year = 126

Assume that the year is not a leap year.

Then 1 year = 365 days

Let the random variable x represent the number of checks he wrote in one​ day.

Then , the mean number of checks wrote by person each days id=s given by :-

`\lambda=(126)/(365)\approx0.3452`

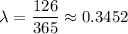
Since , the distribution is Poisson distribution , then the variance must equal to the mean value i.e.
`\sigma^2=\lambda=0.3452`

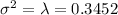
Standard deviation :
`\sigma=√(0.3452)=0.5875372328\approx0.5875`