Question

The shorter leg of a right triangle is 7ft shorter than the longer leg. The hypotenuse is 7ft longer than the longer leg. Find the side lengths of the triangle

Answer 1

Base = 21 ft

Height = 28 ft

Hypotenuse = 35 ft

Explanation:

It is given that,the shorter leg of a right triangle is 7ft shorter than the longer leg. The hypotenuse is 7ft longer than the longer leg

Let longer leg = x then shorter leg = x - 7 and hypotenuse = x+ 7

To find the side lengths of triangle

Here Base = x-7

Height = x

Hypotenuse = x + 7

By using Pythagorean theorem we can write,

Base² + height² = Hypotenuse²

(x - 7)² + x² = (x + 7)²

x² -14x + 49 + x² = x² +14x + 49

x² - 14x = 14x

x² - 28x = 0

x(x - 28) = 0

x = 0 or x = 28

Therefore the value of x = 28

Base = x - 7 = 21

Height = 28

Hypotenuse = 28 + 7 = 35

Answer 2

Hello!

The answers are:

`Hypothenuse=28ft+7ft=35ft\\LongerLeg=28ft\\ShorterLeg=28ft-7ft=21ft`

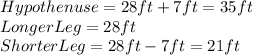
Why?

Since we are working with a right triangle, we can use the Pythagorean Theorem, which states that:

`Hypothenuse^(2)=a^(2)+b^(2)`

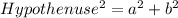
Then, we are given the following information:

Let be "a" the shorter leg and "b" the the longer leg of the right triangle, so:

`(7ft+b)^(2)=(b-7)^(2)+b^(2)`

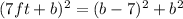
We can see that we need to perform the notable product, so:

`(7ft+b)^(2)=(b-7ft)^(2)+b^(2)\\\\7ft*7ft+2*7ft*b+b^(2)=b^(2)-2*7ft*b+7ft*7ft+b^(2)\\\\49ft^(2) +14ft*b+b^(2)=b^(2)-14ft*b+49ft^(2)+b^(2)\\\\49ft^(2) +14ft*b+b^(2)=-14ft*b+49ft^(2)+2b^(2)\\\\-14ft*b+49ft^(2)+2b^(2)-(49ft^(2) +14ft*b+b^(2))=0\\\\-28ft*b+b^(2)=0\\\\b(-28ft+b)=0`

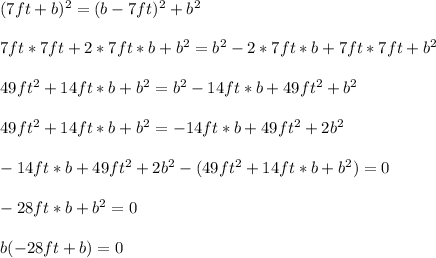
We have that the obtained equation will be equal to 0 if: b is equal to 0 or b is equal to 28:

`0(-28+0)=0`

`28(-28+28)=28(0)=0`

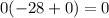
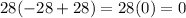
So, since we are looking for the side of a leg, the result that we need its 28 feet.

Hence, we have that the answers are:

`Hypothenuse=28ft+7ft=35ft\\LongerLeg=28ft\\ShorterLeg=28ft-7ft=21ft`

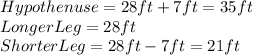
Have a nice day!