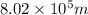Question

A 1,160 kg satellite orbits Earth with a tangential speed of 7,446 m/s. If the satellite experiences a centripetal force of 8,955 N, what is the height of the satellite above the surface of Earth? Recall that Earth’s radius is 6.38 × 106 m and Earth’s mass is 5.97 × 1024 kg.

Answer 1

Answer: The height of the satellite above the surface of Earth is
`8.02* 10^(5)m`

Step-by-step explanation:

Given

Mass of the satellite, m= 1160 kg

tangential speed , v = 7446 m/s

Centripetal force , F = 8955 N

Radius of earth , R=
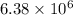`6.38* 10^(6)` m

Let height of satellite above surface of the Earth be H

Centripetal force on satellite is given by

`F=(mv^(2))/(R+H)`

=>
`H=(mv^(2))/(F)-R`

=>
`H=((1160* 7446^(2))/(8955)-6.38* 10^(6)) m=8.02* 10^(5)m`

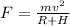
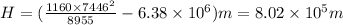
Thus the height of the satellite above the surface of Earth is
`8.02* 10^(5)m`