Answer: Third Option
(2, -1) and (-4, 17)
Explanation:
We have the following system of equations:
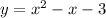
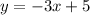
We have the first three steps to solve the system.
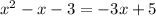 equal both equations
equal both equations
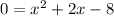 Simplify and equalize to zero
Simplify and equalize to zero
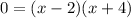 Factorize
Factorize
Then note that the equation is equal to zero when
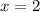 or
or
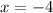
Now substitute the values of x in either of the two situations to obtain the value of the variable y.
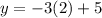
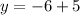
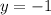
First solution: (2, -1)
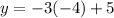
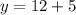
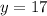
Second solution: (-4, 17)
The answer is the third option