Question

A regular octagon has an apothem measuring 10 in, and a

perimeter of 66.3 in
What is the area of the octagon, rounded to the nearest
square inch?
10 in
88 in 2
175 in 2
332 in2
700 in 2

Answer 1

332 square inch

Explanation:

Solving for an area of a regular octagon, we can make use of the formula shown below:

Area = 1/2 * apothem*perimeter

In this problem, the following values were given such as:

Apothem = 10 inches

Perimeter = 66.3 inches

Solving for the area:

Area = 1/2*10*66.3

Area = 331.5 inches²

The answer is 332.

Answer 2

Option C. 332 in²

Explanation:

In the figure attached, a regular octagon has been drawn with all equal sides and apothem OP = 10 in.

Perimeter of the given octagon is given as 66.3 in

We have to calculate the area of the octagon.

As we can see in the figure an octagon is a combination of 8 triangles.

So we will find the area of one triangle first.

Area of ΔBOC =
`(1)/(2)(BC)(OP)`

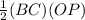
Since perimeter of octagon = 8 × one side = 8×BC

66.3 = 8× BC

BC =
`(66.3)/(8)`

BC = 8.288 in

Therefore, area of ΔBOC =
`(1)/(2)(10)(8.288)`

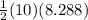
= 5×8.288

= 41.44 in²

Now area of octagon ABCDEFGH = 8×41.44 = 331.5 ≈ 332 in²

Therefore, area of the regular octagon will be 332 in²

Option C. is the answer.