Question

A test score of 48.4 on a test having a mean of 66 and a standard deviation of 11. Find the ​z-score corresponding to the given value and use the ​z-score to determine whether the value is significant. Consider a score to be significant if its ​z-score is less than -2.00 or greater than 2.00. Round the ​z-score to the nearest tenth if necessary. A. -1.6; not significant B.-17.6; significant C. -1.6, significant D. 1.6; not significant

Answer 1

A. -1.6; not significant

Explanation:

The z-score of a data set that is normally distributed with a mean of
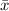`\bar x` and a standard deviation of
`\sigma`, is given by:

`z=(x-\bar x)/(\sigma)`.

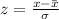From the question, the test score is:
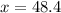`x=48.4`, the mean is
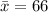`\bar x=66`, and the standard deviation is
`\sigma =11`.

We just have to plug these values into the above formula to obtain:

`z=(48.4-66)/(11)`.

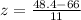This simplifies to:
`z=(-17.6)/(11)`.

`z=-1.6`.

We can see that the z-score falls within two standard deviations of the mean.

Since
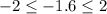`-2\le-1.6\le2` the value is not significant.

The correct answer is A. -1.6; not significant