Answer:
 term = 14336
term = 14336
Explanation:
We are given the first term
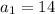 and common ratio
and common ratio
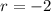 of a geometric sequence and we are to find the
of a geometric sequence and we are to find the
 term of this sequence.
term of this sequence.
We know that the formula to find the
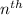 term in a geometric sequence is given by:
term in a geometric sequence is given by:
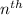 term =
term =

Substituting the given values in the above formula:
 term =
term =
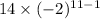
 term =
term =
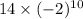
 term = 14336
term = 14336