Answer:
Option D. sine theta equals plus or minus square root of thirty-five over six, tangent theta equals plus or minus square root of thirty five
Explanation:
we have that
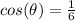
If the cosine is positive, then the angle theta lie on the first or fourth Quadrant
therefore
The sine of angle theta could be positive (I Quadrant) or negative (IV Quadrant) and the tangent of angle theta could be positive (I Quadrant) or negative (IV Quadrant)
step 1
Find
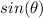
Remember that
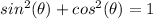
we have
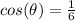
substitute
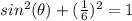
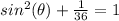
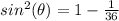
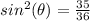
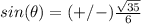
so
sine theta equals plus or minus square root of thirty-five over six
step 2
Find
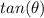
Remember that
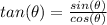
we have
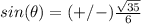
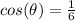
substitute
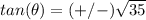
tangent theta equals plus or minus square root of thirty five