Answer:
Option B 3,-3,-6 is correct.
Explanation:
We need to find real zeroes of

Solving
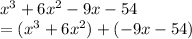
Taking x^2 common from first 2 terms and -9 from last two terms we get
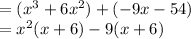
Taking (x+6) common
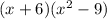
x^2-9 can be solved using formula a^2-b^2 = (a+b)(a-b)
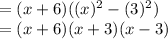
Putting it equal to zero,
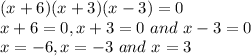
So, Option B 3,-3,-6 is correct.