Question

What are the real zeroes of x3 + 6 x2 – 9x - 54?

A. 1,2, 27
B. 3, -3, -6
c. -6,3, -6
D. 2,-1, 18
E. 3,3, -6

Answer 1

B. 3,-3,-6

Explanation:

Answer 2

Option B 3,-3,-6 is correct.

Explanation:

We need to find real zeroes of
`x^3+6x^2-9x-54`

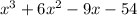
Solving

`x^3+6x^2-9x-54\\=(x^3+6x^2)+(-9x-54)`

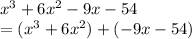
Taking x^2 common from first 2 terms and -9 from last two terms we get

`=(x^3+6x^2)+(-9x-54)\\=x^2(x+6)-9(x+6)\\`

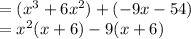
Taking (x+6) common

`(x+6)(x^2-9)\\`

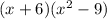
x^2-9 can be solved using formula a^2-b^2 = (a+b)(a-b)

`=(x+6)((x)^2-(3)^2)\\=(x+6)(x+3)(x-3)`

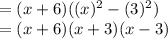
Putting it equal to zero,

`(x+6)(x+3)(x-3) =0\\x+6 =0, x+3=0\,\, and\,\, x-3=0\\x=-6, x=-3\,\, and\,\,  x=3`

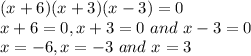
So, Option B 3,-3,-6 is correct.