What is the solution of the equation 4^(x + 1) = 21? Round your answer to the nearest ten-thousandth.

Question

asked May 7, 2020 192k views

2 Answers

Venky Vungarala · Answer 1 · 2020-05-09T23:59:15+0000

Answer:
≈
1.196

Explanation:

Given the equation
4^((x + 1)) = 21 you need to solve for the variable "x".

Remember that according to the logarithm properties:

log_b(b)=1

log(a)^n=nlog(a)

Then, you can apply
log_4 on both sides of the equation:

$log_4(4)^((x + 1)) = log_4(21)\\\\(x + 1)log_4(4) = log_4(21)\\\(x + 1) = log_4(21)$

Apply the Change of base formula:

log_b(x) = (log_a( x))/(log_a(b))

Then you get:

x =(log(21))/(log(4))-1

≈
1.196

Cat · Answer 2 · 2020-05-11T21:38:14+0000

For this case we must solve the following equation:

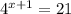
$4 ^ {x + 1} = 21$

We find Neperian logarithm on both sides:

$ln (4 ^ {x + 1}) = ln (21)$

According to the rules of Neperian logarithm we have:

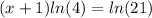
(x + 1) ln (4) = ln (21)

We apply distributive property:

xln (4) + ln (4) = ln (21)

We subtract ln (4) on both sides:

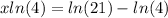
xln (4) = ln (21) -ln (4)

We divide between ln (4) on both sides:

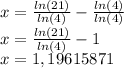
$x = \frac {ln (21)} {ln (4)} - \frac {ln (4)} {ln (4)}\\x = \frac {ln (21)} {ln (4)} - 1\\x = 1,19615871$

Rounding:

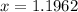
x = 1.1962

Answer:

x = 1.1962