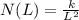Question

Biologists estimate that the number of animal species of a certain body length is inversely proportional to the square of the body length.1 Write a formula for the number of animal species, N, of a certain body length as a function of the length, L. Use k as the constant of proportionality.

Answer 1

Certainly! When we say that the number of animal species \( N \) is inversely proportional to the square of the body length \( L \), what we mean mathematically is that as the body length increases, the number of species decreases at a rate that is the square of the increase in length. This can be represented by the following formula:

\[ N = \frac{k}{L^2} \]

Here \( N \) is the number of species, \( L \) is the body length, and \( k \) is the constant of proportionality. This constant \( k \) represents the number of species at the unit body length (when \( L = 1 \)). The constant of proportionality is determined by the specific biological context, based on empirical data or theoretical considerations.

In this formula, \( L^2 \) denotes the body length squared, and the fraction represents the inverse relationship.

In summary, to find the number of species \( N \) for a given body length \( L \), we use the inverse square relationship with the constant of proportionality \( k \).

Answer 2

`N(L)=(k)/(L^2)`

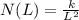
Explanation:

Here, N represents the number of animal species and L represents a certain body length,

According to the question,

`N\propto (1)/(L^2)`

`\implies N=(k)/(L^2)`

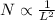
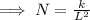
Where, k is the constant of proportionality,

Since, with increasing the value of L the value of N is decreasing,

So, we can say that, N is dependent on L, or we can write N(L) in the place of N,

Hence, the required function formula is,

`N(L)=(k)/(L^2)`