Answer:
the number of employees is decreasing by 10% every year
Explanation:
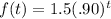
In the given function 1.5 represents the initial number of employees
Exponential function in the form of

When the value of b is less than 1 then it is exponential decay
When the value of b is greater than 1 then it is exponential growth
Exponential decay factor is 0.90
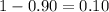
0.10 times 100 = 10%
So the number of employees is decreasing by 10% every year