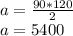Question

Please help me .....

Answer 1

a) c = 150 ft

b) A = 5400 ft²

Explanation:

`a)\ \text{Use the Pythagorean theorem:}\\\\leg^2+leg^2=hypotenuse^2\\\\\text{We have:}\ leg=90\ ft,\ leg=120\ ft,\ hypotenuse=c.\\\\\text{Substitute:}\\\\c^2=90^2+120^2\\\\c^2=8100+14400\\\\c^2=22500\to c=√(22500)\\\\c=150\ ft`

`b)\ \text{The formula of an area of a right triangle:}\\\\A=(ab)/(2)\\\\a,\ b-legs\\\\\text{We have}\ a=90\ ft\ \text{and}\ b=120\ ft.\ \text{Substitute:}\\\\A=((90)(120))/(2)=(90)(60)=5400\ ft^2`

Answer 2

150 feet of flowers would be planted along side C

`a=5400`

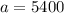
Explanation:

Use the pythagorean theorem to find the length of side C

`a^2+b^2=c^2`

Input the corresponding numbers into the formula

`90^2+120^2=c^2`

`c^2=22500`

`c = √(22500) \\ c=150`

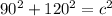
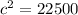
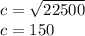
150 feet of flowers would be planted along side C

To find the area multiply the base and height together, and divide the total by two

`a = (bh)/(2)`

`a = (90 * 120)/(2) \\ a=5400`