Answer:
Option A is correct.
Explanation:
We are given:
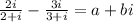
We need to find the value of a.
The LCM of (2+i) and (3+i) is (2+i)(3+i)
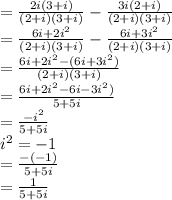
Now rationalize the denominator by multiplying by 5-5i/5-5i
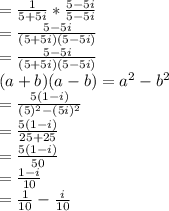
We are given
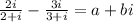
Now after solving we have:
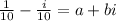
So value of a = 1/10 and value of b = -1/10
So, Option A is correct.