Question

If (2i/2+i)-(3i/3+i)=a+bi, then a=
A. 1/10
B. -10
C. 1/50
D. -1/10​

Answer 1

Option A is correct.

Explanation:

We are given:

`(2i)/(2+i)-(3i)/(3+i) = a+bi`

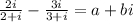
We need to find the value of a.

The LCM of (2+i) and (3+i) is (2+i)(3+i)

`=(2i(3+i))/((2+i)(3+i))-(3i(2+i))/((2+i)(3+i))\\=(6i+2i^2)/((2+i)(3+i))-(6i+3i^2)/((2+i)(3+i))\\=(6i+2i^2-(6i+3i^2))/((2+i)(3+i))\\=(6i+2i^2-6i-3i^2))/(5+5i)\\=(-i^2)/(5+5i)\\i^2=-1\\=(-(-1))/(5+5i)\\=(1)/(5+5i)`

Now rationalize the denominator by multiplying by 5-5i/5-5i

`=(1)/(5+5i)*(5-5i)/(5-5i) \\=(5-5i)/((5+5i)(5-5i))\\=(5-5i)/((5+5i)(5-5i))\\(a+b)(a-b)= a^2-b^2\\=(5(1-i))/((5)^2-(5i)^2)\\=(5(1-i))/(25+25)\\=(5(1-i))/(50)\\=(1-i)/(10)\\=(1)/(10)-(i)/(10)`

We are given

`(2i)/(2+i)-(3i)/(3+i) = a+bi`

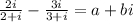
Now after solving we have:

`(1)/(10)-(i)/(10)=a+bi`

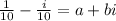
So value of a = 1/10 and value of b = -1/10

So, Option A is correct.