Answer:
Angular velocity of the disk is 8.552 rad/s
Step-by-step explanation:
It is given that,
Rotational kinetic energy, KE = 1280 J
The moment of inertia of the disk, I = 35 kg m²
We have to find the angular velocity of the disk. In rotational mechanics the kinetic energy of the disk is given by :
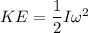
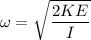
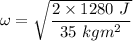
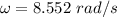
Hence, the angular velocity of the disk is 8.552 rad/s.