Question

Suppose a disk with constant angular velocity has rotational kinetic energy 1280 J. If the moment of inertia of the disk is 35 kg-m^2, then what is its angular velocity? (a) 7.604 rad/s (b) 8.552 rad/s (c) 10.12 rad/s (d) 6.818 rad/s (e) 9.952 rad/s (f) 8.935 rad/s f

Answer 1

Angular velocity of the disk is 8.552 rad/s

Step-by-step explanation:

It is given that,

Rotational kinetic energy, KE = 1280 J

The moment of inertia of the disk, I = 35 kg m²

We have to find the angular velocity of the disk. In rotational mechanics the kinetic energy of the disk is given by :

`KE=(1)/(2)I\omega^2`

`\omega=\sqrt{(2KE)/(I)}`

`\omega=\sqrt{(2* 1280\ J)/(35\ kgm^2)}`

`\omega=8.552\ rad/s`

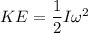
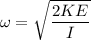
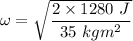
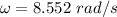
Hence, the angular velocity of the disk is 8.552 rad/s.