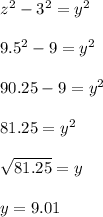Question

Find the value of y and
simplify completely.
y =
?​

Answer 1

y=9.01

Explanation:

In this question you apply the Pythagoras Theorem to generate relationships which will enable you to form equations and solve for the unknown.

The Pythagoras Theorem states that when you have a right-angle triangle and squares are made at each of the three sides, the sum of squares of the two small sides will equal the square of the longest side.

It is expressed as a²+b²=c² where;

• a and b are the shortest sides of the triangle, where b is the height
• c is the longest side of the triangle/hypotenuse

In the question we can use three triangles to form expressions using this theorem

First triangle

• That one with a height of y, short side of 3 and hypotenuse of z

The relationship you can form is;

`3^2+y^2=z^2\\9+y^2=z^2\\y^2=z^2-9------------------------(1)`

In this equation you make y² the subject of the formula

Second Triangle

• The second triangle is that with a base of 27 as the (a), a height of y as the (b) and the hypotenuse of x as the (c)

Hence the relationship you can form is

`27^2+y^2=x^2\\729+y^2=x^2\\y^2=x^2-729`

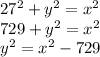
In this equation you make y² the subject of the formula

Third Triangle

• The third triangle is that one with a base of z as (a) , x as (b) which is the height and 30(3+27) as the (c) which is the hypotenuse

The relationship you can form is;

`z^2+x^2=30^2\\x^2=30^2-z^2---------------------(3)`

Here x² is the subject of the formula

Equations

`y^2=z^2-9\\y^2=x^2-729\\x^2=900-z^2`

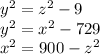
Substitute equation 3 in equation 2

`y^2=x^2-729-------------2\\\\x^2=900-z^2-------------3\\\\y^2=900-z^2-729\\\\y^2=171-z^2---------------4`

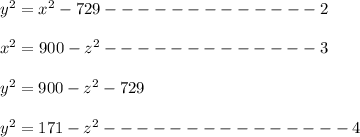
Substitute equation 4 in equation 1

`y^2=171-z^2---------------4\\\\y^2=z^2-9------------1\\\\z^2-9=171-z^2\\\\2z^2=171+9\\\\z^2=180\\\\z=√(180) \\\\z=9.487\\\\z=9.5`

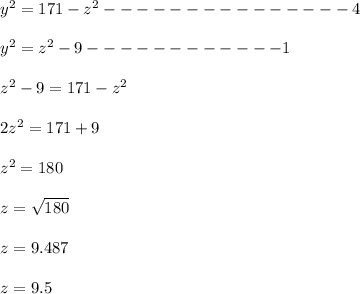
Use the value of z in equation 1 to get value of y

`z^2-3^2=y^2\\\\9.5^2-9=y^2\\\\90.25-9=y^2\\\\81.25=y^2\\\\√(81.25) =y\\\\y=9.01`