Question

What is the probability that a randomly drawn hand of four cards contains all black cards or all face cards? The probability is 6 Round to four decimal places as needed.)

Answer 1

Answer: 0.05699

Explanation:

The total number of cards in a deck = 52

The total number of black cards = 26

Then ,
`\text{P(Black)}=(C(26,4))/(C(52,4))=0.00182842367\approx0.00183`

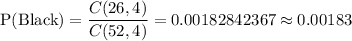
The total number of face cards = 12

Then ,
`\text{P(Face)}=(C(12,4))/(C(52,4))\approx0.05522`

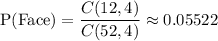
The number of cards that are black and face cards = 6

Then ,
`\text{P(Black and Face )}=(C(6,4))/(C(52,4))\approx0.00006`

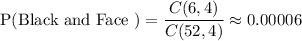
Then , the probability that a randomly drawn hand of four cards contains all black cards or all face cards is given by :-

`\text{P(Black or Face)}=\text{P(Black)+P(Face)-P(Black and Face)}\\\\\Rightarrow\ \text{P(Black or Face)}=0.00183+0.05522-0.00006\\\\\Rightarrow\ \text{P(Black or Face)}=0.05699`