Answer:
Explanation:
Let x = Michael's age.
Then x² = the square of his age
and x² - 12x = the square of his age – 12 times his age
and x² - 12x = 85
We must solve the quadratic for x.
1. Subtract 85 from each side.
x² - 12x - 85 = 0
2. Multiply the leading coefficient and the constant
1 × 85 = 85
3. Find two numbers that multiply to give -85 and add to give -12.
Possible pairs are 1, 85; 5, 17
Start with the numbers near the end of the list.
By trial and error, you will find that 5 and -17 work:
5 ×(-17) = -85
and 5 - 17 = -12
4. Rewrite -12x as 5x -17x
x² + 5x – 17x - 85 =0
5. Factor by grouping the first two and the last two terms
x(x + 5) - 17(x + 5) =0
(x + 5)(x - 17) = 0
6. Find the zeroe
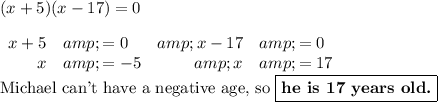
Check:
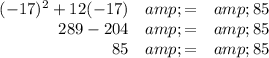
OK.