Answer:
Height of cables = 23.75 meters
Explanation:
We are given that the road is suspended from twin towers whose cables are parabolic in shape.
For this situation, imagine a graph where the x-axis represent the road surface and the point (0,0) represents the point that is on the road surface midway between the two towers.
Then draw a parabola having vertex at (0,0) and curving upwards on either side of the vertex at a distance of
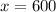 or
or
 , and y at 95.
, and y at 95.
We know that the equation of a parabola is in the form
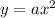 and here it passes through the point
and here it passes through the point
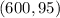 .
.
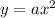
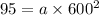
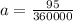
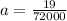
So new equation for parabola would be
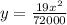 .
.
Now we have to find the height
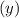 of the cable when
of the cable when
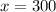 .
.
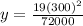
y = 23.75 meters