Question

How do I calculate this? Is there a formula?

A suspension bridge with weight uniformly distributed along its length has twin towers that extend 95 meters above the road surface and are 1200 meters apart. The cables are parabolic in shape and are suspended from the tops of the towers. The cables touch the road surface at the center of the bridge. Find the height of the cables at a point 300 meters from the center. ​ (Assume that the road is​ level.)

Answer 1

Answer: 23.75 meters

Explanation:

If we assume that the origin of the coordinate axis is in the vertex of the parabola. Then the function will have the following form:

`y = a (x-0) ^ 2 + 0\\\\y = ax ^ 2`

We know that when the height of the cables is equal to 95 then the horizontal distance is 600 or -600.

Thus:

`95 = a (600) ^ 2`

`a = \frac{95} {600 ^ 2}\\\\a = \frac {19} {72000}`

Then the equation is:

`y = (19)/(72000) x ^ 2`

Finally the height of the cables at a point 300 meters from the center is:

`y = (19)/(72000)(300) ^ 2`

`y =23.75\ meters`

Answer 2

Height of cables = 23.75 meters

Explanation:

We are given that the road is suspended from twin towers whose cables are parabolic in shape.

For this situation, imagine a graph where the x-axis represent the road surface and the point (0,0) represents the point that is on the road surface midway between the two towers.

Then draw a parabola having vertex at (0,0) and curving upwards on either side of the vertex at a distance of
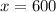`x = 600` or
`x = -600`, and y at 95.

We know that the equation of a parabola is in the form
`y=ax^2` and here it passes through the point
`(600, 95)`.

`y=ax^2`

`95=a * 600^2`

`a=(95)/(360000)`

`a=(19)/(72000)`

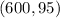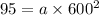
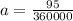
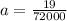
So new equation for parabola would be
`y=(19x^2)/(72000)`.

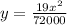Now we have to find the height
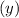`(y)`of the cable when
`x= 300`.

`y=(19 (300)^2)/(72000)`

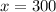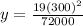
y = 23.75 meters