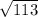Question

What is the distance between the points (2 -3) and (-6 4) on the coordinate plane

Answer 1

√113

or

10.6301458127

Explanation:

Plug the coordinated into this equation and make sure you match up the corrdinates in the correct order

d = √(x2 - x1)^2 + (y2 - y1)^2

The number next to the number does NOT mean multiply it mean like this

(x2, y2) and (x1, y1) so you would plug them in like this:

d = √(-6 - 2)^2 + (4 - (-3))^2

d = √(-8)^2 + (7)^2

d = √(64 + 49

d = √113

or 10.6301458127

Answer 2

Answer with Step-by-step explanation:

The distance(d) between the points (a,b) and (c,d) is given by:

`d=√((c-a)^2+(d-b)^2)`

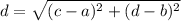
Here, we have to find distance between (2,-3) and (-6,4)

(a,b)=(2,-3) and (c,d)=(-6,4)

`d=√((-6-2)^2+(4-(-3))^2)`

`d=√(8^2+7^2)`

`d=√(64+49)`

`d=√(113)`

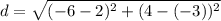
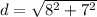
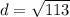
Hence, the distance between the points (2 -3) and (-6 4) on the coordinate plane is:

`√(113)`