Question

What is the cube root of -729a9b6

Answer 1

-9a3b2

Explanation:

Answer 2

`\sqrt[3]{- 729{a}^(9) {b}^(6) } = - 9 {a}^(3) {b}^(2)`

EXPLANATION

We want to find the cube root of

`- 729 {a}^(9) {b}^(6)`

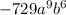
We express this symbolically as:

`\sqrt[3]{- 729 {a}^(9) {b}^(6) }`

The expression under the radical called the radicand.

We need to express this radical in exponential form using the property,

`{x}^{ (m)/(n) } = \sqrt[n]{ {x}^(m) }`

Applying this rule gives us:

`\sqrt[3]{- 729 {a}^(9) {b}^(6) } = ({- 729 {a}^(9) {b}^(6)})^{ (1)/(3) }`

`\sqrt[3]{- 729{a}^(9) {b}^(6) } = ({- {9}^(3) {a}^(9) {b}^(6)})^{ (1)/(3) }`

Recall that

`({a}^(m) )^(n) = {a}^(mn)`

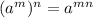
We apply this rule on the RHS to get,

`\sqrt[3]{- 729{a}^(9) {b}^(6) } = ({- {9}^{3 * { (1)/(3) } } {a}^{9 * { (1)/(3) } } {b}^{6 * { (1)/(3) } }})`

This simplifies to

`\sqrt[3]{- 729{a}^(9) {b}^(6) } = - 9 {a}^(3) {b}^(2)`