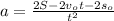Question

In physics, if a moving object has a starting position at so, an initial velocity of vo, and a constant acceleration a, the

the position S at any time t>O is given by:
S = 1/2 at ^2 + vot+so
Solve for the acceleration, a, in terms of the other variables. For this assessment item, you can use^to show exponent
and type your answer in the answer box, or you may choose to write your answer on paper and upload it.

Answer 1

`a=(2S -2v_ot-2s_o)/(t^2)`

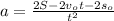
Explanation:

We have the equation of the position of the object

`S = (1)/(2)at ^2 + v_ot+s_o`

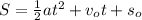
We need to solve the equation for the variable a

`S = (1)/(2)at ^2 + v_ot+s_o`

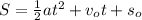
Subtract
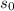`s_0` and
`v_0t` on both sides of the equality

`S -v_ot-s_o = (1)/(2)at ^2 + v_ot+s_o - v_ot- s_o`

`S -v_ot-s_o = (1)/(2)at ^2`

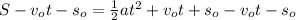
multiply by 2 on both sides of equality

`2S -2v_ot-2s_o = 2*(1)/(2)at ^2`

`2S -2v_ot-2s_o =at ^2`

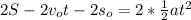
Divide between
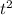`t ^ 2` on both sides of the equation

`(2S -2v_ot-2s_o)/(t^2) =a(t^2)/(t^2)`

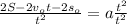
Finally

`a=(2S -2v_ot-2s_o)/(t^2)`