Answer:
The balance after 1 year, 5 years, 10 years, 25 years are 15085.85, 20339.35, 29549.22 and 90609.34 respectively.
Explanation:
It is given that the principle amount is $14,000 and interest rate is 7.47%.
The formula for amount is
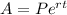
Where, P is principle, r is rate of interest and t is time in years.
Substitute P=14000 and r=0.0747 in the above equation.
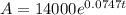 ..... (1)
..... (1)
Substitute t=1 in equation (1) to find the balance after 1 year.
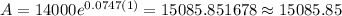
Substitute t=5 in equation (1) to find the balance after 5 year.
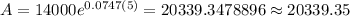
Substitute t=10 in equation (1) to find the balance after 10 year.
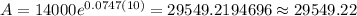
Substitute t=25 in equation (1) to find the balance after 25 year.

Therefore the balance after 1 year, 5 years, 10 years, 25 years are 15085.85, 20339.35, 29549.22 and 90609.34 respectively.