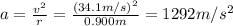Question

An athlete swings a ball, connected to the end of a chain, in a horizontal circle. The athlete is able to rotate the ball at the rate of 8.13 rev/s when the length of the chain is 0.600 m. When he increases the length to 0.900 m, he is able to rotate the ball only 6.04 rev/s. (a) Which rate of rotation gives the greater speed for the ball? 6.04 rev/s 8.13 rev/s (b) What is the centripetal acceleration of the ball at 8.13 rev/s? m/s2 (c) What is the centripetal acceleration at 6.04 rev/s? m/s2

Answer 1

The rate of rotation that gives the greater speed for the ball is 8.13 rev/s. The centripetal acceleration of the ball at 8.13 rev/s is 39.43 m/s^2, while the centripetal acceleration at 6.04 rev/s is 32.90 m/s^2.

Step-by-step explanation:

The rate of rotation that gives the greater speed for the ball is 8.13 rev/s. The speed of the ball is directly proportional to the rate of rotation. So, a higher rate of rotation will result in a greater speed for the ball.

The centripetal acceleration of the ball at 8.13 rev/s can be calculated using the formula:
centripetal acceleration = (angular velocity)^2 * radius
Plugging in the values:
centripetal acceleration = (8.13 rev/s)^2 * 0.6 m = 39.43 m/s^2

The centripetal acceleration of the ball at 6.04 rev/s can be calculated in the same way:
centripetal acceleration = (6.04 rev/s)^2 * 0.9 m = 32.90 m/s^2

Answer 2

(a) 6.04 rev/s

The speed of the ball is given by:

`v=\omega r`

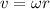
where

`\omega` is the angular speed

r is the distance of the ball from the centre of the circle

In situation 1), we have

`\omega=8.13 rev/s \cdot 2\pi = 51.0 rad/s`

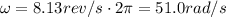
r = 0.600 m

So the speed of the ball is

`v=(51.0 rad/s)(0.600 m)=30.6 m/s`

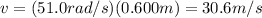
In situation 2), we have

`\omega=6.04 rev/s \cdot 2\pi = 37.9 rad/s`

r = 0.900 m

So the speed of the ball is

`v=(37.9 rad/s)(0.900 m)=34.1 m/s`

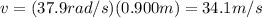
So, the ball has greater speed when rotating at 6.04 rev/s.

(b)
`1561 m/s^2`

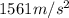
The centripetal acceleration of the ball is given by

`a=(v^2)/(r)`

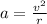
where

v is the speed

r is the distance of the ball from the centre of the trajectory

For situation 1),

v = 30.6 m/s

r = 0.600 m

So the centripetal acceleration is

`a=((30.6 m/s)^2)/(0.600 m)=1561 m/s^2`

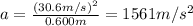
(c)
`1292 m/s^2`

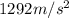
For situation 2 we have

v = 34.1 m/s

r = 0.900 m

So the centripetal acceleration is

`a=(v^2)/(r)=((34.1 m/s)^2)/(0.900 m)=1292 m/s^2`