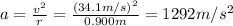(a) 6.04 rev/s
The speed of the ball is given by:
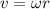
where
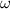 is the angular speed
is the angular speed
r is the distance of the ball from the centre of the circle
In situation 1), we have
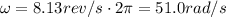
r = 0.600 m
So the speed of the ball is
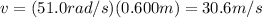
In situation 2), we have
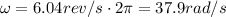
r = 0.900 m
So the speed of the ball is
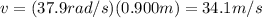
So, the ball has greater speed when rotating at 6.04 rev/s.
(b)
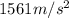
The centripetal acceleration of the ball is given by
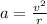
where
v is the speed
r is the distance of the ball from the centre of the trajectory
For situation 1),
v = 30.6 m/s
r = 0.600 m
So the centripetal acceleration is
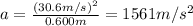
(c)
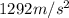
For situation 2 we have
v = 34.1 m/s
r = 0.900 m
So the centripetal acceleration is