Answer:
Option c.
Explanation:
The given expression is
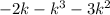
We need to find the factor form of the given expression.
Taking out HCF.
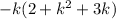
Arrange the terms according to there degree.
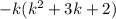
Splitting the middle terms we get
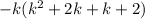
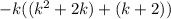
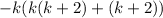
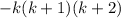
The factor form of given expression is -k(k+1)(k+2). Therefore, the correct option is c.