Question

Which of the following is the equation of a circle whose center is at the origin and whose radius is 4?

Answer 1

x²+y²=16

Explanation:

the general equation for a circle is given as :

(x−h)²+(y−k)²=r²

where (h, k) is the coordinate of the center of the circle and r is the radius

in this case h=0, k=0 and r = 4

equation becomes

x²+y²=4²

or

x²+y²=16

Answer 2

Answer: Last option.

Explanation:

The equation of a circle in Center-radius form is:

`(x-h)^2+(y-k)^2=r^2`

Where the center is at the point (h,k) and "r" is the radius.

If the center of this circle is at the origin, means that:

`h=0\\k=0`

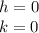
Since the radius is 4, then:

`r=4`

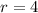
Now we need to substitute these values into the equation of the circle.

`(x-0)^2+(y-0)^2=(4)^2`

Simplifying the equation, we get:

`x^2+y^2=16`

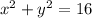
This matches with the last option.