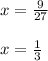What is the value of x if 9x^-1 - 2 = 25

Question

asked Oct 13, 2020 206k views

2 Answers

Ivan Koblik · Answer 1 · 2020-10-19T07:18:37+0000

Answer:

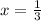
Explanation:

You need to remember the Negative exponent rule:

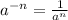
a^(-n)=(1)/(a^n)

Then, having the equation
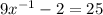9x^(-1) - 2 = 25 , you can rewrite it in this form:

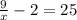
(9)/(x) - 2 = 25

Now add 2 to both sides of the equation:

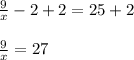
$(9)/(x) - 2+2 = 25+2\\\\(9)/(x)=27$

Multiply both sides of the equation by "x":

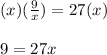
$(x)((9)/(x))=27(x)\\\\9=27x$

And finally divide both sides of the equation by 27.

The value of "x" is:

$x=(9)/(27)\\\\x=(1)/(3)$