Question

Jacob is practicing javelin throws. He throws the javelin from a height of 6 feet. The height of the javelin, h(x), in relation to the horizontal distance that it covers, x, can be modeled by a quadratic function.

Each of the following functions is a different form of the quadratic model for this situation. Which form is most helpful in determining the horizontal distance the javelin covers?

A. h(x)= -0.01(x-150)(x+4)
B. h(x)= -0.01(x-73)^2+ 59.29
C. h(x)= -0.01x(x-146)+6
D. h(x)= -0.01x^2+1.46x+6

Answer 1

The answer is A

Explanation:

I am 100% sure cuz I just did the test:)

Answer 2

Answer: Option A

`h(x) = -0.01 (x-150) (x + 4)`

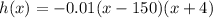
Explanation:

The javelin will have reached its maximum horizontal distance when it touches the ground.

Then the maximum horizontal distance occurs when the height h (x) is equal to zero.

So we must equal h(x) to zero and solve the equation for x.

Therefore the form that is most useful to determine the horizontal distance that the javelin covers is the one that is factored. Because it allows us to find the zeros of the quadratic function more easily

`h(x) = -0.01 (x-150) (x + 4) = 0`

`-0.01 (x-150) (x + 4) = 0`

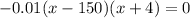
The equation is equal to zero when
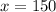`x = 150` or when
`x = -4`

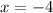
Therefore the solution is
`x = 150`.

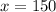The horizontal distance that covers the javelin is 150 feet