To graph the function h(x) = 8|x+1| - 1, plot key points at (-3, 15), (-1, -1), and (1, 15). The graph exhibits vertical stretching due to the coefficient 8 and symmetry around the line x = -1.
To graph the function (h(x) = 8|x+1| - 1), follow these steps:
1. Identify Key Points:
Determine critical points where the expression inside the absolute value becomes zero. Here, when (x = -1), (h(x) = -1). Additionally, consider points on either side of -1.
2. Plot Points:
Plot these points on the coordinate plane: (-3, 15), (-1, -1), and (1, 15).
3. Determine Behavior:
Understand that the absolute value function |x+1| ensures symmetry around the vertical line x = -1. The coefficient 8 stretches the graph vertically, and the constant -1 shifts it downward.
4. Connect Points:
Draw a smooth curve connecting the points, considering the shape of the absolute value function.
5. Label Axes:
Label the x-axis and y-axis appropriately.
The resulting graph represents the function
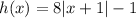 .
.