Answer:
Explanation:
Our equations are

Let us understand the term Discriminant of a quadratic equation and its properties
Discriminant is denoted by D and its formula is
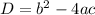
Where
a= the coefficient of the

b= the coefficient of

c = constant term
Properties of D: If D
i) D=0 , One real root
ii) D>0 , Two real roots
iii) D<0 , no real root
Hence in the given quadratic equations , we will find the values of D Discriminant and evaluate our answer accordingly .
Let us start with
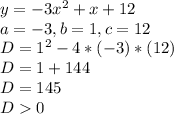
Hence we have two real roots for this equation.

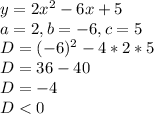
Hence we do not have any real root for this quadratic
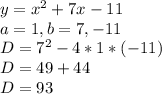
Hence D>0 and thus we have two real roots for this equation.
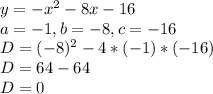
Hence we have one real root to this quadratic equation.