Question

Write an equation for the given function given the period, phase shift, and vertical shift.

cotangent function, period = π, phase shift = -1/3 π, vertical shift = 2.

Answer 1

`y = \cot(x - (\pi)/(3) ) + 2`

Step-by-step explanation

The cotangent function that is fully transformed is of the form

`y =a \cot(bx + c) + d`

where 'a' is the amplitude.

`(\pi)/(b) = \pi`

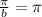
is the period.

This implies that b=1

The phase shift is

`(c)/(b) = - (\pi)/(3)`

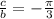
Substitute b=1 to get;

`c = - (\pi)/(3)`

and d=2 is the vertical shift.

We choose a=1 to get the required function as

`y = \cot(x - (\pi)/(3) ) + 2`