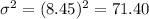Question

Adimas found the mean of her 11 math test scores for the first semester.

x = ≈ 81
Using 81 as the mean, find the variance of her grades rounded to the nearest hundredth.

σ2 =

Find the standard deviation of her grades rounded to the nearest hundredth.

σ =

Answer 1

Answer: O^2= 71.36

O=8.45

Answer 2

The complete question is attached.

To find the variance and deviation, we have to use their definition or formulas:

Standard deviation.

`\sigma=\sqrt{(\sum (x- \mu)^(2) )/(N)}`

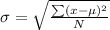
So, first we have to find the difference between each number and the mean:

76-81=-5

87-81=6

65-81=-16

88-81=7

67-81=-14

84-81=3

77-81=-4

82-81=1

91-81=10

85-81=4

90-81=9

Now, we have to elevate each difference to the squared power and then sum all:

`25+36+256+49+196+9+16+1+100+16+81=785`

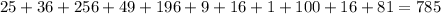
Then, we replace in the formula:

`\sigma=\sqrt{(785)/(11)} \approx 8.45`

Variance.

The variance is just the squared power of the standard deviation. So:

`\sigma^(2)=(8.45)^(2)=71.40`