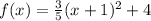Answer:
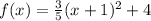
Explanation:
The equation of a quadratic function in vertex form is given by:
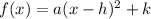
Where (h,k) is the vertex.
It was given in the question that the vertex of the parabola is (-1,4).
When we substitute the vertex into the formula we get:
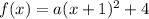
The parabola also passes through (4,19) hence it must satisfy its equation.

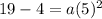
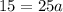
We divide both sides by 25 to get:
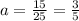
Hence the quadratic function is: