Answer:
53
Explanation:
Let's make some equations.
The number is two-digit, so let's make it
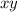
Also, the two digits add up to 8, so
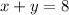
Now the value of
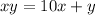
and the value of
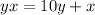
Since we know that when we reverse the digits the number is less than the resulting number by 18, we can formulate an equation.

Solve this equation.
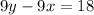


Now let's use the equation we made earlier.
Change
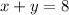 into
into
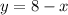
Solve the system of equations.

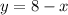
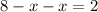
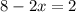
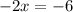

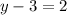
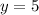
So the original number is 53.