Answer:
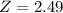 and this Z-score is “unusual.”
and this Z-score is “unusual.”
Explanation:
To calculate the Z score use the following formula

Where
μ is the average
 is the standard deviation
is the standard deviation
x is the data to which we will calculate the z-score
In this case
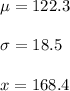
So
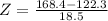
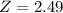
A z-score is unusual if
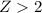 or
or
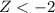
Finally
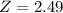 and this Z-score is “unusual.”
and this Z-score is “unusual.”