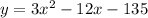Question

HELP please urgent!! - PLEASE CLICK, NEED HELP -

Write a quadratic function in standard form whose graph passes through (-5,0), (9,0), and (8, -39).


f(x) =

Answer 1

`y=3x^2-12x-135`

Explanation:

The standard form of a quadratic is
`y=ax^2+bx+c`

We will use the x and y values from each of our 3 points to find a, b, and c. Filling in the x and y values from each point:

First point (-5, 0):

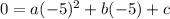`0=a(-5)^2+b(-5)+c` and

0 = 25a - 5b + c

Second point (9, 0):

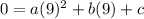`0=a(9)^2+b(9)+c` and

0 = 81a + 9b + c

Third point (8, -39):

`-39=a(8)^2+b(8)+c` and

-39 = 64a + 8b + c

Use the elimination method of solving systems on the first 2 equations to eliminate the c. Multiply the first equation by -1 to get:

-25a + 5b - c = 0

81a + 9b + c = 0

When the c's cancel out you're left with

56a + 14b = 0

Now use the second and third equations and elimination to get rid of the c's. Multiply the second equation by -1 to get:

-81a - 9b - c = 0

64a + 8b + c = -39

When the c's cancel out you're left with

-17a - 1b = -39

Between those 2 bolded equations, eliminate the b's. Do this by multiplying the second of the 2 by 14 to get:

56a + 14b = 0

-238a - 14b = -546

When the b's cancel out you're left with

-182a = -546 and

a = 3

Use this value of a to back substitute to find b:

56a + 14b = 0 so 56(3) + 14b = 0 gives you

168 + 14b = 0 and 14b = -168 so

b = -12

Now back sub in a and b to find c:

0 = 25a - 5b + c gives you

0 = 75+ 60 + c so

0 = 135 + c and

c = -135

Put that all together into the standard form equation to get

`y=3x^2-12x-135`

Answer 2

f(x) = 3x^2 -12x -135

Explanation:

The given zeros tell you that two factors are (x +5) and (x -9). Then the function can be written ...

f(x) = a(x +5)(x -9)

We can find "a" from ...

f(8) = -39 = a(8 +5)(8 -9) = -13a

3 = a . . . . . . divide by -13

Expanding the above form, we get the standard form ...

f(x) = 3x^2 -12x -135