Answer:
b=12 , a=6
 , c=6
, c=6

Explanation:
based on the graph you are showing, you can use "SOH CAH TOA"
for right triangles, then you use "CAH" for get b:
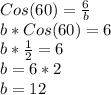
you do the same for a, but in this case you use sin, not cos:
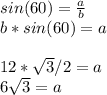
and with your b value, you can get c, but now you use Cos with the 45 angle:

remember SOH CAH TOA means, Sin(x)=opposite/Hypotenuse, Cos(x)=adjacent/hypotenuse, and tan(x)=Opposite/adjacent.