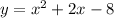Question

Write a function to model the data

x row consists of: -4, -2, 0, 2, 4

y row consists of: 0, -8, -8, 0, 16

The function is y =

Answer 1

`y=x^2+2x-8`

Explanation:

When you graph those points on a piece of graph paper it appears that the points are in the form of a positive x^2 parabola, which has the standard form

`y=ax^2+bx+c`

We just need to solve for a, b, and c. Easy. We have 3 points from the table. We will use all three of them to find the values of a, b, and c.

Use the points (0, -8), (2, 0), and (4, 16). You can use any points, but I chose the one with an x value of 0 for a good reason, and chose the other 2 because I don't like too many negatives!

Use the first point in those above to solve for c:

`-8=a(0)^2+b(0)+c`

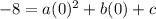
From this you solve for c: c = -8

Now use the next point along with the value of c to find another equation:

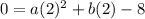`0=a(2)^2+b(2)-8` and

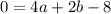`0=4a+2b-8` so

8 = 4a + 2b

That equation will be used again in a minute.

Use the last point to solve for yet another equation (stay with me...we are almost there!):

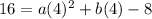`16=a(4)^2+b(4)-8` and

24 = 16a + 4b

Now we will use the method of elimination to solve for b:

8 = 4a + 2b

24 = 16a + 4b

Multiply the first equation by -4 to eliminate the a terms:

-32 = -16a - 8b

24 = 16a + 4b

leaves you with

-4b = -8 and b = 2. Now plug that back in to solve for a:

If 8 = 4a + 2b, then 8 = 4a + 2(2) and 8 = 4a + 4

4a = 4 and a = 1

Again, your equation is

`y=x^2+2x-8`