Answer:
This does represent an exponential function , because his savings increase by a constant rate
Explanation:
Let
x -----> the number of weeks
y ----> the amount saved
In this problem we have a exponential function of the form
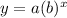
where
a is the initial value
b is the base
r is the rate of change
where
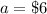
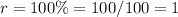 ---- because he doubles the amount each week
---- because he doubles the amount each week
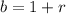 ---->
---->
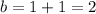
substitute
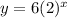
therefore
This does represent an exponential function , because his savings increase by a constant rate