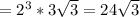Question

Simplest form to write
(2×6)³/²

Answer 1

Answer:
`24√(3)`

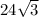
Explanation:

You need to remember that
`\sqrt[n]{a}` can be written in the following for:

`a^{(1)/(n)}`

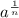
Knowing this and given the expression
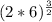`(2*6)^{(3)/(2)}`, you need to multiply the numbers inside the parentheses:

`(12)^{(3)/(2)}`

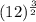
Rewrite it in this form:

`=√(12^3)==√(1,728)`

Descompose 1,728 into its prime factors:

`1,728=2*2*2*2*2*2*3*3*3=2^6*3^3`

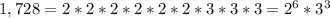
Applying the Product of power property, which states that:

`(a^m)(a^n)=a^((m+n))`

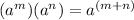
You can say that:

`=√(1,728)=√(2^6*3^2*3)`

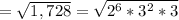
Simplifying, you get:

`=2^3*3√(3)=24√(3)`